Source : B-trees and database indexes

B-trees and database indexes

By Benjamin Dicken | September 9, 2024

What is a B-tree?

The B-tree plays a foundational role in many pieces of software, especially database management systems (DBMS). MySQL, Postgres, MongoDB, Dynamo, and many others rely on B-trees to perform efficient data lookups via indexes. By the time you finish this article, you’ll have learned how B-trees and B+trees work, why databases use them for indexes, and why using a UUID as your primary key might be a bad idea. You’ll also have the opportunity to play with interactive animations of the data structures we discuss. Get ready to click buttons.

B-treeは、特にデータベース管理システム(DBMS)で重要な役割を果たしています。MySQL、Postgres、MongoDB、Dynamoなど多くのシステムがB-treeを使ってインデックスによる効率的なデータ検索を行っています。この記事を読み終えると、B-treeとB+treeの仕組み、なぜデータベースがインデックスにそれらを使うのか、プライマリキーにUUIDを使うのが良くない理由などを学べるでしょう。また、議論する データ構造のインタラクティブなアニメーションを試すこともできます。ボタンをクリックしながら、理解を深めていきましょう。

Computer science has a plethora of data structures to choose from for storing, searching, and managing data on a computer. The B-tree is one such structure, and is commonly used in database applications. B-trees store pairs of data known as keys and values in what computer programmers call a tree-like structure. For those not acquainted with how computer scientists use the term “tree” it actually looks more like a root system.

コンピューター科学には、コンピューター上でデータを保存、検索、管理するために使える多くのデータ構造があります。B-treeはそのようなデータ構造の1つで、データベースアプリケーションでよく使われています。B-treeは、キーと値のペアを、コンピューターサイエンティストが「ツリー構造」と呼ぶ形式で保持しています。「ツリー」という言葉を慣れていない人にとっては、むしろ根っこの系統のように見えるかもしれません。

Below you’ll find the first interactive component of this blog. This allows you to visualize the structure of a B-tree and see what happens as you add key/value pairs and change the number of key/value pairs per node. Give it a try by clicking the Add or Add random button a few times and try to get an intuitive sense of how it works before we move on to the details.https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#btree

ここに、このブログの最初のインタラクティブコンポーネントがあります。これを使うと、B-treeの構造を視覚化し、キー/値のペアを追加したり、ノードあたりのキー/値のペア数を変更したりしたときの変化を確認できます。

「追加」や「ランダムに追加」ボタンを数回クリックして、詳細に進む前に、B-treeの仕組みについて直感的な理解を深めてみてください。

If the animations above are too fast or slow, you can adjust the animation speed of everything that happens with the B-trees in this article. Adjust below:https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#btree-speed-adjuster

上記のアニメーションが速すぎたり遅すぎたりする場合は、このサイト内のB-treeに関するすべてのアニメーションの速度を調整することができます。以下のリンクからアニメーションの速度を調整してください:

Every B-tree is made up of nodes (the rectangles) and child pointers (the lines connecting the nodes). We call the top-most node the root node, the nodes on the bottom level leaf nodes, and everything else internal nodes. The formal definition of a B-tree can vary depending on who you ask, but the following is a pretty typical definition.

B-treeは、ノード(長方形)とチャイルドポインター(ノードを接続する線)から構成されています。一番上のノードを「ルートノード」、一番下のレベルのノードを「リーフノード」、その間のノードを「内部ノード」と呼びます。B-treeの正式な定義は、誰に聞くかによって異なりますが、一般的には以下のようなものです。

A B-tree of order K is a tree structure with the following properties:

A B-treeのorder Kとは、以下のような特性を持つツリー構造のことです:

• Each node in the tree stores N key/value pairs, where N is greater than 1 and less than or equal to K.
  • 各ノードには N 個のキー/値のペアが格納されており、N は 1 より大きく K 以下の整数です
• Each internal node has at least N/2 key/value pairs (an internal node is one that is not a leaf or the root).
  • 内部ノード(ルートノードとリーフノード以外)には、最低でも N/2 個のキー/値のペアが格納されています。
• Each node has N+1 children.
  • 各ノードには N+1 個の子ノードがあります。
• The root node has at least one value and two children, unless it is the sole node.
  • ルートノードには、唯一のノードである場合を除いて、最低でも1つの値と2つの子ノードがあります。
• All leaves are on the same level.
  • すべてのリーフノードが同じレベルにあります。

The other key characteristic of a B-tree is ordering. Within each node the elements are kept in order. Any child to the left of a key must only contain other keys that are less than it. Children to the right must have keys that are greater than it.

B-treeのもう一つの重要な特徴は「順序性」です。各ノード内で、要素は順序良く保持されています。ある要素の左側の子ノードには、その要素より小さい要素しか含まれません。一方、右側の子ノードには、その要素より大きい要素が含まれます。

（個人メモ）つまり、B-treeの各ノード内部では順序が保たれており、左から右に要素が大きくなっていくというルールが適用されている。

This enforced ordering means you can search for a key very efficiently. Starting at the root node, do the following:
この順序に従ったデータ構造により、キーの検索を非常に効率的に行えます。

1. Check if the node contains the key you are looking for.
   • ノード内に検索対象のキーが含まれているかを確認する
2. If not, find the location in the node where your key would get inserted into, if you were adding it.
   • 含まれていない場合は、検索キーが挿入されるべき位置を特定する
3. Follow the child pointer at this spot down to the next level, and repeat the process.
   • その位置の子ポインターを辿って、次のレベルのノードに移動する

When searching in this way, you only need to visit one node at each level of the tree to search for one key. Therefore, the fewer levels it has (or the shallower it is), the faster searching can be performed. Try searching for some keys in the tree below:https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#btree-search

この方法で検索を行うと、1つのキーを検索するのに、ツリーの各レベルを1つずつ訪れればよいだけです。つまり、ツリーの階層が浅いほど、検索の速度が速くなります。以下のリンクのツリーで、いくつかのキーを検索してみてください:

B-trees are uniquely suited to work well when you have a very large quantity of data that also needs to be persisted to long-term storage (disk). This is because each node uses a fixed number of bytes. The number of bytes can be tailored to play nicely with disk blocks.

B-treeは、大量のデータを長期ストレージ(ディスク)に永続化する必要がある場合に非常に適しています。その理由は、B-treeの各ノードが固定サイズのバイト数を使うからです。このバイト数は、ディスクブロックのサイズに合わせて調整できます。つまり、B-treeは大容量データの管理と、ディスクアクセスの高速化を両立できるデータ構造なのです。

Reading and writing data on hard-drive disks (HDDs) and solid-state disks (SSDs) is done in units called blocks. These are typically byte sequences of length 4096, 8192, or 16384 (4k, 8k, 16k). A single disk will have a capacity of many millions or billions of blocks. RAM on the other hand is typically addressable on a per-byte level.

ハードディスク(HDD)やソリッドステートディスク(SSD)へのデータの読み書きは、ブロックと呼ばれる単位で行われます。これらのブロックのサイズは、一般的に4,096バイト、8,192バイト、16,384バイト(4KB、8KB、16KB)が一般的です。1つのディスクには数百万から数十億ものブロックが存在します。一方、RAM(メインメモリ)はバイト単位でアドレス指定できるのが一般的です。

This is why B-trees work so well when we need to organize and store persistent data on disk. Each node of a B-tree can be sized to match the size of a disk block (or a multiple of this size).

こちらは、永続的なデータをディスク上に整理して保存する必要があるときに、B-treeがうまく機能する理由です。B-tree の各ノードのサイズは、ディスクブロックのサイズ(またはその倍数)に合わせて設定できます。

The number of values each node of the tree can store is based on the number of bytes each is allocated and the number of bytes consumed by each key / value pair. In the example above, you saw some pretty small nodes — ones storing 3 integer values and 4 pointers. If our disk block and B-tree node is 16k, and our keys, values, and child pointers are all 8 bits, this means we could store 682 key/values with 683 child pointers per node. A three level tree could store over 300 million key/value pairs (682 × 682 × 682 = 317,214,568).

B-tree の各ノードが格納できる値の数は、各ノードに割り当てられたバイト数と、各キー/値のペアが消費するバイト数に基づいています。上記の例では、3つの整数値と4つのポインタを格納する比較的小さなノードが表示されていました。ディスクブロックとB-tree のサイズが16kで、キー、値、子ポインタが全て8ビットの場合、ノードあたり682個のキー/値と683個の子ポインタを格納できます。3レベルの木構造では、3億1,721万4,568個の key/value ペアを格納できます(682 × 682 × 682 = 317,214,568)。

The B+Tree

B-trees are great, but many database indexes use a “fancier” variant called the B+tree. It’s similar to a B-tree, with the following changes to the rules:

B+treeは、B-treesに基づいた「より高度な」バリアントで、多くのデータベースのインデックスで使用されています。B+treeはB-treesに似ていますが、以下のようなルールの変更点があります:

• Key/value pairs are stored only at the leaf nodes.
  • キー/値のペアは leaf ノードにのみ格納される
• Non-leaf nodes store only keys and the associated child pointers.
  • Non-Leaf ノードには、キーと関連する子ポインタのみが格納される

There are two additional rules that are specific to how B+trees are implemented in MySQL indexes:

MySQL のインデックスにおけるB+treeの実装には、以下の2つの追加のルールがあります:

• Non-leaf nodes store N child pointers instead of N+1.
  • Non-leaf ノードは N+1個の子ポインタではなく、N個の子ポインタを格納する
• All nodes also contain “next” and “previous” pointers, allowing each level of the tree to also act as a doubly-linked list.
  • すべてのノードに「次」と「前」のポインタが含まれており、各レベルのツリーがdoubly-linked list として機能できるようになっている

Here’s another visualization showing how the B+tree works with these modified characteristics. This time you can individually adjust the number of keys in inner nodes and in the leaf nodes, in addition to adding key/value pairs. https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree

B+tree のこれらの修正された特性がどのように機能するかを示す別の視覚化ツールです。このツールでは、キー/値のペアを追加するだけでなく、内部ノードとLeaf ノードのキーの数を個別に調整することができます。

Why are B+trees better for databases? There are two primary reasons.
B+tree がデータベースに適している主な2つの理由は以下のとおりです。

1. Since inner nodes do not have to store values, we can fit more keys per inner node! This can help keep the tree shallower.
   • 内部ノードにはキーのみを格納すればよいため、1つのノードあたりより多くのキーを保持できる。これによりツリーの深さを浅くできる。
2. All of the values can be stored at the same level, and traversed in-order via the bottom-level linked list.
   • すべての値は最下層の葉ノードに格納され、下位レベルのリンクリストを順次辿ることで効率的に検索できる。

Go ahead and give searching on a B+tree a try as well:https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree-search

B+trees in MySQL

MySQL, arguably the world’s most popular database management system, supports multiple storage engines. The most commonly used engine is InnoDB which relies heavily on B+trees. In fact, it relies so heavily on them that it actually stores all table data in a B+tree, with the table’s primary key used as the tree key.

世界で最も人気のあるデータベース管理システムの1つであるMySQLは、複数のストレージエンジンをサポートしています。最も一般的に使用されているエンジンはInnoDBで、InnoDBは B+treeに大きく依存しています。実際、InnoDBは B+treeにあまりにも強く依存しているため、テーブルのプライマリキーをツリーのキーとして使用し、すべてのテーブルデータをB+treeに格納しています。

Whenever you create a new InnoDB table you are required to specify a primary key. Database administrators and software engineers often use a simple auto-incrementing integer for this value. Behind the scenes, MySQL + InnoDB creates a B+tree for each new table created. The keys for this tree are whatever the primary key was set to. The values are the remaining column values for each row, and are stored only in the leaf nodes.

InnoDBテーブルを新規作成する際、プライマリキーの指定が必須です。多くの場合、データベース管理者やソフトウェアエンジニアは、単純なauto-incrementing integer 型をプライマリキーとして使用します。その背景では、MySQL + InnoDBが新規作成されたテーブルごとにB+treeを作成します。このツリーのキーは、設定されたプライマリキーになり、値は各行の残りのカラム値となり、Leaf ノードにのみ格納されます。

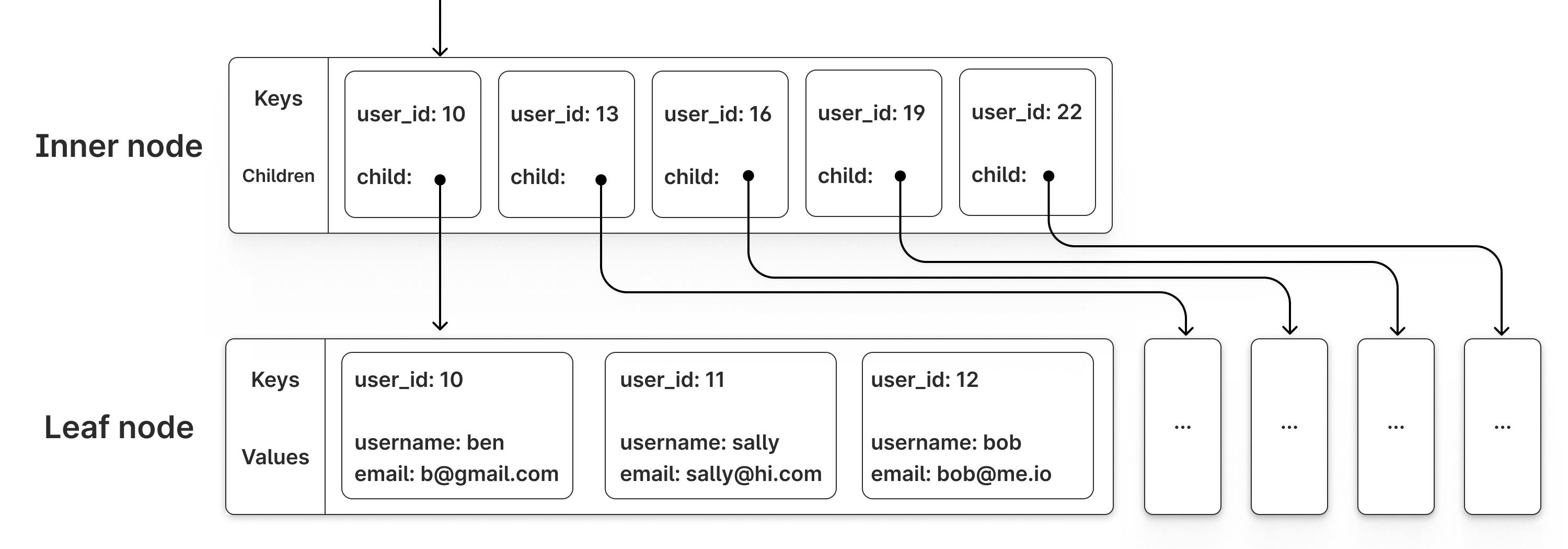
The size of each node in these B+trees is set to 16k by default. Whenever MySQL needs to access a piece of data (keys, values, whatever), it loads the entire associated page (B+tree node) from disk, even if that page contains other keys or values it does not need.

InnoDBが使用するB+treeのノードサイズは、デフォルトで16kに設定されています。MySQL がデータにアクセスする際(キー、値、その他のデータ)、必要なキーや値が含まれているページ(B+treeのノード)全体をディスクから読み込みます。つまり、その時点で必要としない他のキーや値も同時に読み込まれることになります。

The number of rows stored in each node depends on how “wide” the table is. In a “narrow” table (a table with few columns), each leaf could store hundreds of rows. In a “wide” table (a table with many columns), each leaf may only store a single-digit number of rows. InnoDB also supports rows being larger than a disk block, but we won’t dig into that in this post.

InnoDBのB+treeノード内に格納できる行数は、テーブルの”wide”によって決まります。”narrow”テーブル(カラム数が少ない)の場合、1つの葉ノードに数百行を格納できます。一方、”広い”テーブル(カラム数が多い)の場合、1つの葉ノードに1桁台の行数しか格納できません。また、InnoDBでは、1行のデータサイズがディスクブロックサイズを超えることも対応可能ですが、今回は深入りしないことにします。

Use the visualization below to see how the number of keys in each inner node and in each leaf node affect the depth of the tree. The deeper the tree, the slower it is to look up elements. Thus, we want shallow trees for our databases!https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree-depth-line

B+treeのツリー深さに関する影響を視覚化したツールを試してみましょう。ツリーが深くなるほど、要素の検索が遅くなります。したがって、データベースでは浅いツリー構造を持つことが望ましいのです。

It’s also common to create secondary indexes on InnoDB tables — ones on columns other than the primary key. These may be needed to speed up WHERE clause filtering in SQL queries. An additional persistent B+tree is constructed for each secondary index. For these, the key is the column(s) that the user selected the index to be built for. The values are the primary key of the associated row. Whenever a secondary index is used for a query:

InnoDBテーブルでは、主キー以外のカラムにセカンダリインデックスを作成することも一般的です。
これらは、SQLクエリのWHERE句によるフィルタリングを高速化するために必要となる場合があります。各セカンダリインデックスごとに、追加の永続的なB+treeが構築されます。
これらの場合、キーはユーザーがインデックスを作成するために選択したカラムです。
値は、対応する行の主キーです。セカンダリインデックスがクエリで使用されるたびに:

1. A search is performed on the secondary index B+tree.
   • セカンダリインデックスのB+treeで検索が実行されます。
2. The primary keys for matching results are collected.
   • 一致する結果の主キーが収集されます。
3. These are then used to do additional B+tree lookup(s) on the main table B+tree to then find the actual row data.
   • それらは次に、メインテーブルのB+treeで追加のB+tree検索に使用され、実際の行データが見つけられます

Consider the following database schema:

CREATE TABLE user (
  user_id BIGINT UNSIGNED AUTO_INCREMENT NOT NULL,
  username VARCHAR(256) NOT NULL,
  email VARCHAR(256) NOT NULL,
  PRIMARY KEY (user_id)
);
CREATE INDEX email_index ON user(email);

This will cause two B+tree indexes to be created:

• One for the table’s primary key, using user_id for the key and the other two columns stored in the values.
  • 1つはテーブルのプライマリキー用で、キーに「user_id」を使用し、他の2つのカラムの値を格納しています。
• Another for the email_index, with email as the key and user_id as the value.
  • もう1つは「email_index」用のセカンダリインデックスで、キーに「email」を、値に「user_id」を格納しています。

When a query like this is executed:

SELECT username FROM user WHERE email = '[email protected]';

This will first perform a lookup for [email protected] on the email_index B+tree. After it has found the associated user_id value it will use that to perform another lookup into the primary key B+tree, and fetch the username from there.

まず、「email_index」のB+treeに格納されている「[email protected]」をルックアップします。そこで見つかった「user_id」の値を使って、次にプライマリキーのB+treeをルックアップし、そこから「username」を取得します。

Overall, we’d like to always minimize the number of blocks / nodes that need to be visited to fulfill a query. The fewer nodes we have to visit, the faster our query can go. The primary key you choose for a table is pivotal in minimizing the number of nodes we need to visit.

全体としては、クエリを完了するために訪れる必要のあるブロック/ノードの数を常に最小限に抑えたいということです。訪れるノード数が少ないほど、クエリの処理速度が速くなります。そのため、テーブルのプライマリキーの選択が、訪れるノード数を最小化する上で非常に重要になってきます。

Insertions

The way your table’s data is arranged in a B+tree depends on the key you choose. This means your choice of PRIMARY KEY will impact the layout on disk of all of the data in the table, and in turn performance. Choose your PRIMARY KEY wisely!

テーブルのデータがB+treeに配置される方法は、選択するキーによって異なります。つまり、選択するプライマリキーが、テーブル内のすべてのデータのディスク上のレイアウトに影響を与え、ひいては性能にも影響を及ぼします。プライマリキーの選択は慎重に行う必要があります。

Two common choices for a primary key are:

• An integer sequence (such as BIGINT UNSIGNED AUTO_INCREMENT)
  • 整数シーケンス (BIGINT UNSIGNED AUTO_INCREMENT のような)
• A UUID, of which there are many versions.
  • UUID (バージョンは多数存在)

Let’s first consider the consequences of using a UUIDv4 primary key. A UUIDv4 is a mostly-random 128 bit integer.

まず、UUIDv4をプライマリキーとして使う場合の影響について考えてみましょう。UUIDv4は、ほぼランダムな128ビットの整数です。

We can simulate this by inserting a bunch of random integers into our B+tree visualization. On each insertion, all of the visited nodes will be highlighted green. You can also control the percentage of keys to keep in the existing node when a split occurs. Give it a try by clicking the Add random button several times. What do you notice?https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree-random
それでは、B+treeの視覚化ツールを使って、ランダムな整数をたくさん挿入してみましょう。挿入時に、訪れたノードがすべて緑色でハイライトされます。また、ノードが分割される際の、既存ノードに残すキーの割合も調整できます。「Add random」ボタンを何度か押して試してみてください。どのようなことがわかりますか?

A few observations:

1. The nodes visited for an insert are unpredictable ahead of time.
   • 挿入時に訪れるノードは事前に予測できない
2. The destination leaf node for an insert is unpredictable.
   • 挿入先のLeaf ノードも事前に予測できない
3. The values in the leaves are not in order.
   • Leaf ノードの値は順序付けられていない

Issues 1 and 2 are problematic because over the course of many insertions we’ll have to visit many of the nodes (pages) in the tree. This excessive reading and writing leads to poor performance. Issue 3 is problematic if we intend to ever search for or view our data in the order it was inserted.

1, と 2. の問題点は、多くの挿入操作を行うと、ツリー内の多くのノード(ページ)を訪れる必要があり、この過剰な読み書きがパフォーマンスの低下につながることです。3. の問題点は、データを挿入順に検索したり表示したりする際に、データが順序付けられていないことが支障となる可能性があるということです。

The same problem can arise (albeit in a less extreme way) with some other UUIDs as well. For example, UUID v3 and v5 are both generated via hashing, and therefore will not be sequential and have similar behavior to inserting randomly. Alternatively, UUIDv7 actually does a good job of overcoming some of these challenges.

UUIDの場合でも、同様の問題が生じる可能性があります。例えば、UUIDv3とv5はハッシュ値を使って生成されるため、順序性がなく、ランダムに挿入した場合と同様の挙動になります。一方、UUIDv7は、これらの課題を一定程度解決している良い選択肢となっています。

Let’s consider using a sequential BIGINT UNSIGNED AUTO_INCREMENT as our primary key instead. Try inserting sequential values into the B+tree instead:https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree-sequential

BIGINT UNSIGNED AUTO_INCREMENTのような順次増加する整数型をプライマリキーとして使うことを検討してみましょう。

This mitigates all of the aforementioned problems:

1. We always follow the right-most path when inserting new values.
   • 新しい値を挿入する際は、常に最右のパスを辿る
2. Leaves only get added on the right side of the tree.
   • Leaf ノードは常に木の右側に追加される
3. At the leaf level, data is in sorted order based on when it was inserted.
   • Leaf ノードのレベルでは、データが挿入された順番に従って昇順に並んでいる

Because of 1 and 2, many insertions happening in sequence will revisit the same path of pages, leading to fewer I/O requests when inserting a lot of key/value pairs.

1 と 2 があるため、連続して多くの挿入を行うと、同じページのパスが再訪問されるため、キーと値のペアを大量に挿入する場合の I/O 要求が少なくなります。

The bar chart below shows the number of unique nodes visited for the previous 5 inserts on the two B+trees above. Assuming trees of the same depth, you should see random one being slightly higher, meaning worse performance.https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree-insert-bar-chart

下の棒グラフは、上の2つのB+treeで過去5回のインサートでアクセスしたユニークノードの数を示しています。同じ深さのツリーを仮定すると、ランダムなツリーが少し高くなり、パフォーマンスが低下するはずです。

If you are curious about the effect of the split percentage on sequential vs random insert patterns, check out the interactive visualization below. Use the slider to set the split percentage. The line graph will update to show how many nodes needed to be visited for the prior 5 at various points in a 400-key insertion sequence. Notice that in most cases, the sequential inserts require much fewer node visits than random inserts, and are also more predictable.https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree-inserts-nodes-visited

分割パーセンテージがシーケンシャルインサートパターンとランダムインサートパターンに及ぼす影響について知りたい場合は、以下のインタラクティブなビジュアライゼーションをご覧ください。スライダーを使用して分割率を設定します。折れ線グラフが更新され、400 キーの挿入シーケンスのさまざまなポイントで過去 5 つのノードにアクセスする必要があったノードの数が表示されます。ほとんどの場合、連続挿入はランダム挿入よりも必要なノード訪問数がはるかに少なく、予測も容易であることに注意してください。https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree-inserts-nodes-visited

Data order

It’s common to search for data from a database in time-sequenced order. Consider viewing the timeline on X, or a chat history in Slack. We typically want to see the posts and chat messages in time (or reverse-time) sequences. This means we’ll often read chunks of database that are “near” each other in time. These queries take the form:

データベースからデータを時系列で検索するのが一般的です。X でタイムラインを表示したり、Slack でチャット履歴を表示したりすることを検討してください。私たちは通常、投稿やチャットメッセージを時系列 (または逆時間) で確認したいものです。つまり、時間的に互いに「近く」位置にあるデータベースの断片を読み取ることが多いということです。これらのクエリの形式は次のとおりです。

SELECT username, message_text, ...
FROM post
  WHERE sent > $START_DATETIME
  AND sent < $END_DATETIME
  ORDER BY sent DESC;

Consider what this would be like if we have UUIDv4s for our primary key. In the B+tree below, a bunch of random keys and corresponding values have been inserted into the table. Try finding ranges of values. What do you see?https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree-random-range-search

主キーにUUIDv4があるとしたらどうなるか考えてみてください。以下のB+tree では、ランダムなキーとそれに対応する値がテーブルに挿入されています。値の範囲を探してみてください。何が見える？

Notice that the value sequences are spread out across many non-sequential leaf nodes. On the other hand, consider finding sequentially inserted values instead.https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree-sequential-range-search

値のシーケンスは、連続していない多くの Leaf ノードに分散していることに注意してください。一方、代わりに順番に挿入された値を見つけることを検討してください。

In such cases, all pages with the search results will be next to each other. It’s even possible to search for several rows, and all of them will be next to each other in a single page. For this variety of query pattern, we can mitigate the number of pages that need to be read using a sequential primary key.

このような場合、検索結果を含むすべてのページが隣り合って表示されます。複数の行を検索することも可能で、すべての行が 1 つのページで隣り合って表示されます。このような種類のクエリパターンでは、シーケンシャルなプライマリキーを使用することで読み込む必要のあるページ数を減らすことができます。

Primary key size

Another important consideration is key size. We always want our primary keys to be:

もう 1 つ重要な考慮事項は、キーサイズです。私たちは常にPrimaryキーを以下のようにしたいと思っています。

1. Big enough to never face exhaustion
   • 枯渇しない(キーの値が使い切られてしまう)
2. Small enough to not use excessive storage
   • ストレージを過剰に使用しない

For integer sequences, we can sometimes get away with a MEDIUMINT (16 million unique values) or INT (4 billion unique values) for smaller tables. For big tables, we often jump to BIGINT to be safe (18 sextillion possible values). BIGINTs are 64 bits (8 bytes). UUIDs are typically 128 bits (16 bytes), twice the size of even the largest integer type in MySQL. Since B+tree nodes are a fixed size, a BIGINT will allow us to fit more keys per-node than UUIDs. This results in shallower trees and faster lookups.

整数シーケンスの場合、MEDIUMINT (1,600 万個のユニーク値) や INT (40 億個のユニーク値) で済むことがあります。大きなテーブルでは、安全を確保するために BIGINT にジャンプすることがよくあります (18 兆個の可能な値)。BIGINT は 64 ビット (8 バイト) です。UUID は通常 128 ビット (16 バイト) で、MySQL で最大の整数型の 2 倍のサイズです。B+tree ノードは固定サイズなので、BIGINT を使うと UUID よりも多くのキーをノードあたりに収めることができます。その結果、ツリーが浅くなり、検索が速くなります。

Consider a case where each tree node is only 100 bytes, child pointers are 8 bytes, and values are 8 bytes. We could fit 4 UUIDs (plus 4 child pointers) in each node. Hit the play insertion sequence button below to see the inserts.https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree-key-size-large

各ツリーノードがわずか100バイト、子ポインタが8バイト、値が8バイトの場合を考えてみましょう。各ノードには 4 つの UUID (および 4 つの子ポインタ) を入れることができます。下の挿入シーケンスを再生ボタンを押すと、挿入内容が表示されます。

If we had used a BIGINT instead, we could fit 6 keys (and corresponding child pointers) in each node instead. This would lead to a shallower tree, better for performance.https://planetscale.com/blog/btrees-and-database-indexes/iframe.html#bplustree-key-size-small

代わりに BIGINT を使用した場合、代わりに各ノードに 6 つのキー (および対応する子ポインタ) を配置できます。これにより、ツリーが浅くなり、パフォーマンスが向上します。

Pages and InnoDB

Recall that one of the big benefits of a B+tree is the fact that we can set the node size to whatever we want. In InnoDB, the B+tree nodes are typically set to 16k, the size of an InnoDB page.

B+tree の大きな利点の 1 つは、ノードサイズを自由に設定できることであることを思い出してください。InnoDB では、B+ツリーのノードは通常、InnoDB ページのサイズである 16k に設定されています。

When fulfilling a query (and therefore traversing B+trees), InnoDB does not read individual rows and columns from disk. Whenever it needs to access a piece of data, it loads the entire associated page from disk.

クエリを実行する (つまり B+Tree をトラバースする) 場合、InnoDB はディスクから個々の行と列を読み取りません。データにアクセスする必要があるときはいつでも、関連するページ全体をディスクからロードします。

InnoDB has some tricks up its sleeve to mitigate this, the main one being the buffer pool. The buffer pool is an in-memory cache for InnoDB pages, sitting between the pages on-disk and MySQL query execution. When MySQL needs to read a page, it first checks if it’s already in the buffer pool. If so, it reads it from there, skipping the disk I/O operation. If not, it finds the page on-disk, adds it to the buffer pool, and then continues query execution.

InnoDBにはこれを軽減するためのいくつかのトリックがありますが、主なものはバッファープールです。バッファープールは InnoDB ページのメモリ内キャッシュで、ディスク上のページと MySQL クエリの実行の間にあります。MySQL はページを読み取る必要がある場合、まずそのページが既にバッファープールにあるかどうかを確認します。その場合は、ディスク I/O 操作をスキップして、そこから読み込みます。そうでない場合は、ディスク上でページを見つけてバッファープールに追加し、クエリの実行を続行します。

The buffer pool drastically helps query performance. Without it, we’d end up doing significantly more disk I/O operations to handle a query workload. Even with the buffer pool, minimizing the number of pages that need to be visited helps performance (1) because there’s still a (small) cost to looking up a page in the buffer pool, and (2) it helps reduce the number of buffer pool loads and evictions that need to take place.

バッファプールはクエリのパフォーマンスを大幅に向上させます。これがないと、クエリのワークロードを処理するために行うディスク I/O 操作が大幅に増えることになります。バッファープールがあっても、訪問する必要のあるページ数を最小限に抑えることでパフォーマンスが向上します。(1) バッファープールでページを検索するのに (少し) コストがかかるため、(2) バッファープールのロードとエビクションの回数を減らすことができます。

Other situations

Here, we mostly focused on comparing a sequential key to a random / UUID key. However, the principles shown here are useful to keep in mind no matter what kind of primary or secondary key you are considering.

ここでは、主にシーケンシャルキーとランダム/ UUIDキーを比較することに焦点を当てました。ただし、ここで示した原則は、どのような主キーまたは二次キーを検討しているかにかかわらず、覚えておくと役に立ちます。

For example, you may also consider using a user.created_at timestamp as a key for an index. This will have similar properties to a sequential integer. Insertions will generally always go to the right-most path, unless legacy data is being inserted.

たとえば、user.created_at タイムスタンプをインデックスのキーとして使用することを検討することもできます。これは連続した整数と似た性質を持つことになります。レガシーデータを挿入しない限り、通常、挿入は常に右端のパスに行われます。

Conversely, something like a user.email_address string will have more similar characteristics to a random key. Users won’t be creating accounts in email-alphabetical order, so insertions will happen all over the place in the B+tree.

逆に、user.email_address 文字列のようなものは、ランダムキーと似た特性を持ちます。ユーザーは電子メールのアルファベット順にアカウントを作成しないため、B+ ツリーのいたるところで挿入が行われます。

Conclusion

This is already a long blog post, and yet, much more could be said about B+trees, indexes, and primary key choice in MySQL. On the surface it may seem simple, but there’s an incredible amount of nuance to consider if you want to squeeze every ounce of performance out of your database. If you’d like to experiment further, you can visit the dedicated interactive B+tree website. If you want a regular B-tree, go here instead. I hope you learned a thing or two about indexes!

これはすでに長いブログ記事ですが、MySQLのB+ツリー、インデックス、主キー選択についてはさらに多くのことが言えます。一見シンプルに見えるかもしれませんが、データベースからパフォーマンスを最大限に引き出したいなら、考慮すべき微妙な違いが数多くあります。さらに試してみたい場合は、専用のインタラクティブな B+Tree Web サイトをご覧ください。通常のBツリーが必要な場合は、代わりにこちらにアクセスしてください。インデックスについて、1、2 つのことを学んだといいですね。